Pojęcie funkcji odwrotnej do danej

(1)

Pojęcie funkcji odwrotnej do

danej

Autorzy:

Anna Barbaszewska-Wiśniowska

(2)

Pojęcie funkcji odwrotnej do danej

Autor: Anna Barbaszewska-Wiśniowska

DEFINICJA

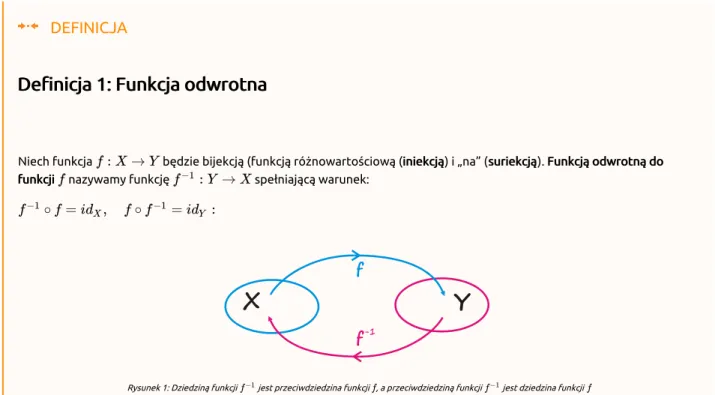
Definicja 1: Funkcja odwrotna

Niech funkcja będzie bijekcją (funkcją różnowartościową (iniekcjąiniekcją) i „na” (suriekcjąsuriekcją). Funkcją odwrotną doFunkcją odwrotną do funkcji

funkcji nazywamy funkcję spełniającą warunek:

Rysunek 1: Dziedziną funkcji jest przeciwdziedzina funkcji , a przeciwdziedziną funkcji jest dziedzina funkcji

f : X → Y

f

−1

: Y → X

∘ f = i , f ∘

= i :

f

−1

_d

_X

_f

−1

_d

_Y

(3)

UWAGA

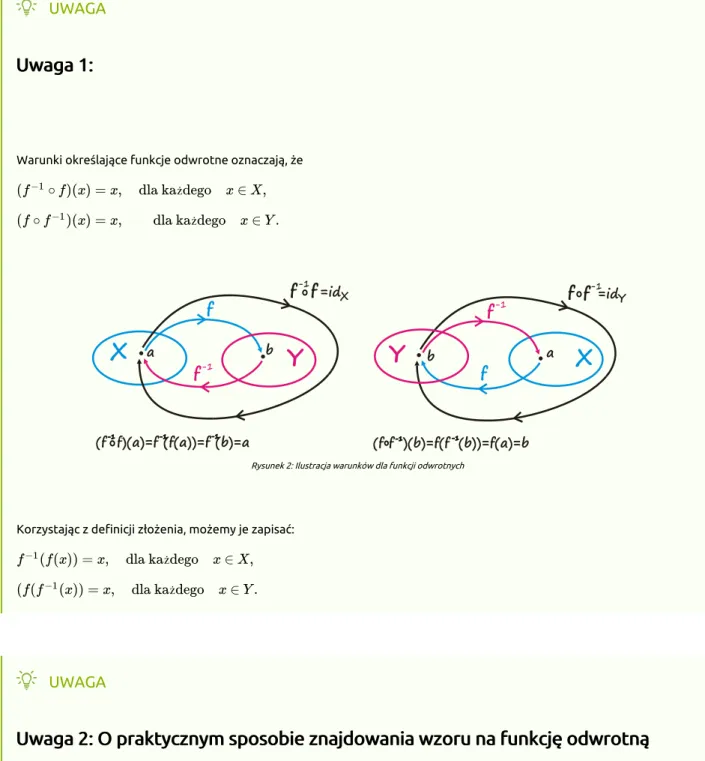
Uwaga 1:

Warunki określające funkcje odwrotne oznaczają, że

Rysunek 2: Ilustracja warunków dla funkcji odwrotnych

Korzystając z definicji złożenia, możemy je zapisać:

UWAGA

Uwaga 2: O praktycznym sposobie znajdowania wzoru na funkcję odwrotną

Aby podać wzór na funkcję odwrotną, funkcję daną traktujemy jako zbiór par uporządkowanych

i zmieniamy kolejność w tych parach tzn. tworzymy zbiór . W praktyce oznacza to wyliczenie ze wzoru i zamianę w otrzymanym wzorze roli z . Mamy wówczas , czyli funkcję

(

f

−1

∘ f)(x) = x, dla ka

ż

dego x ∈ X,

(f ∘

f

−1

)(x) = x,

dla ka

ż

dego x ∈ Y .

(f(x)) = x, dla ka

ż

dego x ∈ X,

f

−1

(f(

f

−1

(x)) = x, dla ka

ż

dego x ∈ Y .

x ↦ f(x)

{(x, y) : y = f(x)}

{(y, x) : y = f(x)}

x

y = f(x)

x =

f

−1

(y)

_{x y}

_{y =}

_f

−1

_(x)

: x ↦ y =

(x).

f

−1

_f

−1

(4)

PRZYKŁAD

Przykład 1:

Sprawdzimy, że funkcja jest odwrotna do funkcji . Rozwiązanie

Rozwiązanie

Oznaczmy przez , , , . Sprawdzimy, że złożenie w obie strony funkcji i jest identycznością na .

Odpowiedź Odpowiedź

Dane funkcje są wzajemnie odwrotne.

ZADANIE

Zadanie 1:

Treść zadania: Treść zadania:

Zbadamy, czy istnieje funkcja odwrotna do funkcji

i w przypadku odpowiedzi pozytywnej wyznaczymy tę funkcję odwrotną. Narysujemy wykresy i .

Rozwiązanie: Rozwiązanie:

Najpierw sprawdzimy, czy jest iniekcją. Wykorzystamy warunek równoważny definicji iniekcji. Mamy pokazać, że dla każdych dwóch elementów , z tego, że wynika, że .

Obierzmy więc dwie liczby i i załóżmy, że . Ostatnia równość przybiera tu postać:

Z założenia wynika, że .

Funkcja jest więc iniekcją.

x ↦ 2x − 6

x ↦ x + 3

1₂

f(x) = 2x − 6 f : R → R g(x) = x + 3

1 2

g : R → R

f

g

R

(g ∘ f)(x) = g(f(x)) = g(2x − 6) = (2x − 6) + 3 = x − 3 + 3 = x,

1 2

(f ∘ g)(x) = f(g(x)) = f( x + 3) = 2 ( x + 3) − 6 = x + 6 − 6 = x.

1 2 12

f : [3, ∞) → [1, ∞), f(x) = (x − 3 + 1,

)

2

f f

−1

f

, ∈

= [3, ∞)

x

1

x

2

D

f

f( ) = f( )

x

1

x

2

x

1

=

x

2

> 3

x

1

x

2

> 3

f( ) = f( )

x

1

x

2

( − 3 + 1 = ( − 3 + 1

x

1

)

2

x

2

)

2

( − 3 = ( − 3

x

1

)

2

x

2

)

2

=

,

( − 3

x

1

)

2

−

−−−−−

−

√

( − 3

−

x

−−−−−

2

)

−

2

| − 3| = | − 3|.

x

1

x

2

> 3

x

1

| − 3| =

x

1

x

1

− 3

> 3

x

2

| − 3| =

x

2

x

2

− 3

− 3 =

− 3,

x

1

x

2

= .

x

1

x

2

f

[1, ∞)

(5)

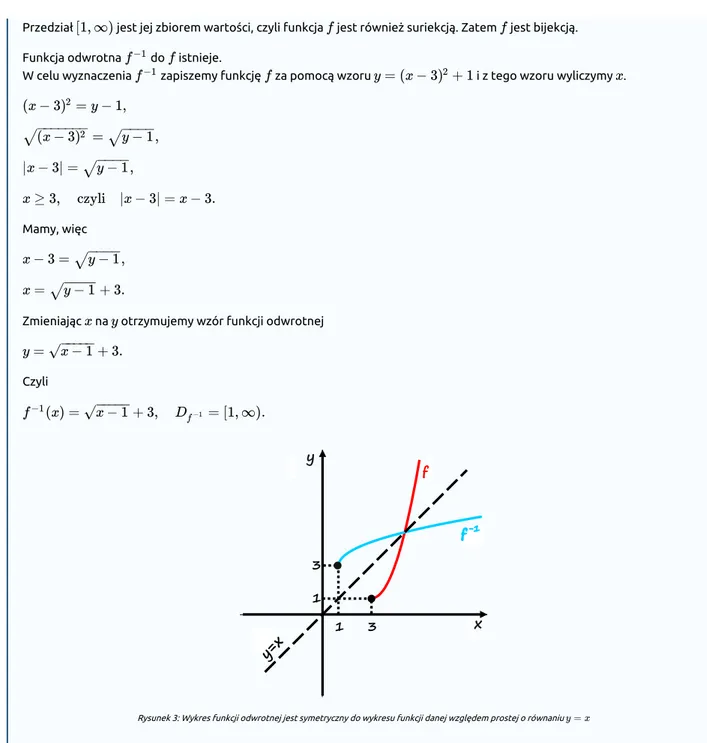
Przedział jest jej zbiorem wartości, czyli funkcja jest również suriekcją. Zatem jest bijekcją. Funkcja odwrotna do istnieje.

W celu wyznaczenia zapiszemy funkcję za pomocą wzoru i z tego wzoru wyliczymy .

Mamy, więc

Zmieniając na otrzymujemy wzór funkcji odwrotnej

Czyli

Rysunek 3: Wykres funkcji odwrotnej jest symetryczny do wykresu funkcji danej względem prostej o równaniu

Odpowiedź Odpowiedź

Funkcją odwrotna do jest taka, że

TWIERDZENIE

Twierdzenie 1: O monotoniczności funkcji odwrotnej

Funkcja odwrotna do funkcji rosnącej jest rosnąca. Funkcja odwrotna do funkcji malejącej jest malejąca.

[1, ∞)

f

−1

_f

f

−1

_f

_{y = (x − 3 + 1}

₎

2

_x

(x − 3 = y − 1,

)

2

=

,

(x − 3)

2

−

−−−−−

−

√

− −

y − 1

−−

|x − 3| =

√

− −

y − 1

−−

,

x ≥ 3, czyli |x − 3| = x − 3.

x − 3 =

√

− −

y − 1

−−

,

x =

√

− −

y − 1

−−

+ 3.

x y

y =

√

− −

x − 1

−−−

+ 3.

(x) =

+ 3,

= [1, ∞).

f

−1

_√

− −

_{x − 1}

−−−

_D

f−1 y = x

f

−1

: [1, ∞) → [3, ∞),

f

−1

(x) =

+ 3.

f

−1

_√

− −

_{x − 1}

−−−

(6)

PRZYKŁAD

Przykład 2: Funkcja logarytmiczna i wykładnicza jako funkcje wzajemnie do siebie

odwrotne

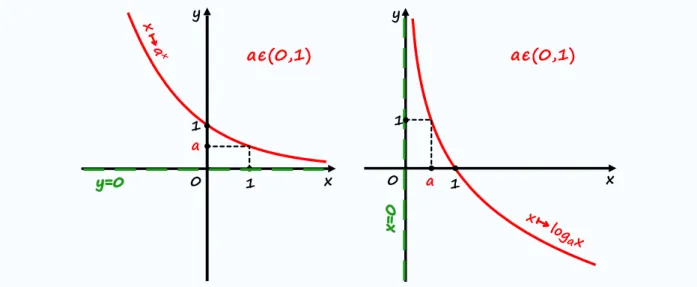
Rysunek 4: Funkcja wykładnicza o podstawie większej od jest funkcją rosnącą. dwrotna do niej funkcja logarytmiczna o tej samej podstawie jest również funkcja rosnącą.

Rysunek 5: Funkcja wykładnicza o podstawie ułamkowej jest funkcją malejącą. Odwrotna do niej funkcja logarytmiczna o tej samej podstawie jest również malejąca

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

a 1

(7)

Data generacji dokumentu: 2019-04-15 02:50:27

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=20d0c353fe5bff29e7e98cfe1864f72d