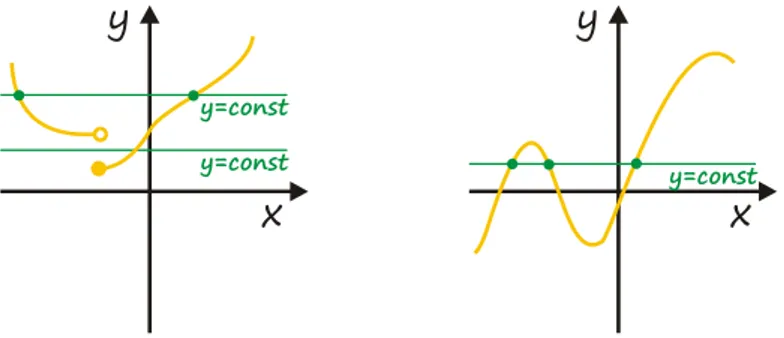Suriekcja, iniekcja, bijekcja

Suriekcja, iniekcja, bijekcja

Autorzy:

Anna Barbaszewska-Wiśniowska

Suriekcja, iniekcja, bijekcja

Suriekcja, iniekcja, bijekcja

Autor: Anna Barbaszewska-Wiśniowska

DEFINICJA

Definicja 1: Suriekcja czyli funkcja „na”

Definicja 1: Suriekcja czyli funkcja „na”

Mówimy, że jest suriekcjąsuriekcją, (czyli funkcją „na”funkcją „na”) wtedy i tylko wtedy, gdy jej zbiór wartości jest równy zbiorowi końcowemu .

Zapisujemy wówczas co odczytujemy: funkcja funkcja prowadzi ze zbioru prowadzi ze zbioru na zbiór na zbiór .

UWAGA

Uwaga 1:

Uwaga 1:

Wiemy, że geometrycznie zbiór wartości funkcji jest rzutem prostopadłym wykresu na oś . Stąd jest suriekcją, gdy rzut jej wykresu na oś pokrywa się ze zbiorem .

Rysunek 1: suriekcja

Rysunek 2: nie jest suriekcją

f : X → Y

Y

f : X

−→

Y

f

X

Y

0y⃗

f : X → Y

0y⃗

Y

PRZYKŁAD

Przykład 1:

Przykład 1:

Niech , . Zbadamy, czy , jest suriekcją. Rozwiązanie

Rozwiązanie Szkicujemy wykres .

Rysunek 3: Wykres funkcji

Z wykresu odczytujemy, że zbiór wartości funkcji (rzut jej wykresu na oś ) to przedział , który jest silnie zawarty w zbiorze , zatem nie jest suriekcją.

ZADANIE

Zadanie 1:

Zadanie 1:

Niech , . Zbadamy czy , jest suriekcją.

Rozwiązanie: Rozwiązanie:

Wykres funkcji powstaje poprzez przesunięcie „w poziomie” o wektor wykresu funkcji wykładniczej , więc rzuty prostopadłe na oś obu wykresów są identyczne. Obie funkcje mają te same zbiory wartości. Wiedząc, że zbiór wartości funkcji wykładniczej jest przedziałem równym całemu zbiorowi wnioskujemy, że jest suriekcją.

INFORMACJA DODATKOWA

Informacja dodatkowa 1:

Informacja dodatkowa 1:

Własność suriektywności zależy od tego, jaki zbiór przyjmiemy za zbiór końcowy . Gdybyśmy w przykładzie 1 jako wzięli przedział funkcja byłaby suriekcją. W szczególności: każda funkcja może być traktowana jako suriekcja na swójkażda funkcja może być traktowana jako suriekcja na swój zbiór wartości zbiór wartości.

X = R Y = (−∞, 3]

f : X → Y f(x) = 2 − |x|

f

f

0y⃗

(−∞, 2]

(−∞, 3]

f

X = R Y = (0, ∞)

f : X → Y f(x) = 3

f

v⃗

= [5, 0]

x → 3

0y⃗

x → 3

_{(0, ∞)}

_Y

_f

Y

Y

(−∞, 2]

DEFINICJA

Definicja 2: Funkcja różnowartościowa, iniekcja

Definicja 2: Funkcja różnowartościowa, iniekcja

Mówimy, że jest iniekcjąiniekcją (funkcją różnowartościowąfunkcją różnowartościową) wtedy i tylko wtedy, gdy dla każdych elementów stąd, że wynika, że Interpretacja geometryczna różnowartościowości.

Funkcja jest różnowartościowa gdy dowolna prosta pozioma o równaniu przecina wykres w co najwyżej jednym punkcie.

Rysunek 4: Funkcje różnowartościowe. Każda prosta pozioma przecina wykres w co najwyżej jednym punkcie

Rysunek 5: Funkcje nieróżnowartościowe. Istnieją proste poziome przecinające wykres w kilku punktach

PRZYKŁAD

Przykład 2:

Przykład 2:

Funkcje logarytmiczna, wykładnicza, funkcja potęgowa postaci dla nieparzystych, są różnowartościowe. Nie są różnowartościowe funkcje trygonometryczne i funkcje potęgowe postaci dla -parzystych.

TWIERDZENIE

Twierdzenie 1:

Twierdzenie 1: Warunek równoważny różnowartościowości

Warunek równoważny różnowartościowości

Funkcja jest funkcją różnowartościową wtedy i tylko wtedy, gdy dla każdych dwóch elementów zachodzi warunek: stąd, że wynika, że .

f : X → Y

, ∈ X

x

x

x

≠

x

f( ) ≠ f( )

x

x

f

y = const

f

y = x

_n

y = x

_n

f : X → Y

x

, ∈ X

x

f( ) = f( )

x

x

x

=

x

DEFINICJA

Definicja 3: Funkcja różnowartościowa na zbiorze

Definicja 3: Funkcja różnowartościowa na zbiorze

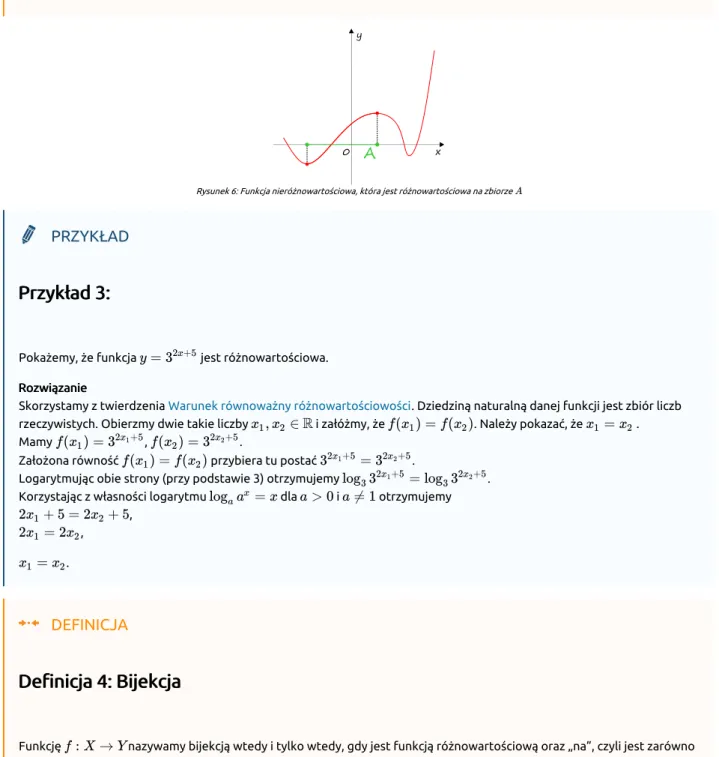
Mówimy, że funkcja funkcja jest różnowartościowa w zbiorze różnowartościowa w zbiorze zawartym w dziedzinie zawartym w dziedzinie wtedy i tylko wtedy, gdy jej restrykcja do zbioru jest funkcja różnowartościową.

Rysunek 6: Funkcja nieróżnowartościowa, która jest różnowartościowa na zbiorze

PRZYKŁAD

Przykład 3:

Przykład 3:

Pokażemy, że funkcja jest różnowartościowa. Rozwiązanie

Rozwiązanie

Skorzystamy z twierdzenia Warunek równoważny różnowartościowości. Dziedziną naturalną danej funkcji jest zbiór liczb rzeczywistych. Obierzmy dwie takie liczby i załóżmy, że . Należy pokazać, że .

Mamy , .

Założona równość przybiera tu postać .

Logarytmując obie strony (przy podstawie 3) otrzymujemy . Korzystając z własności logarytmu dla i otrzymujemy

, , .

DEFINICJA

Definicja 4: Bijekcja

Definicja 4: Bijekcja

Funkcję nazywamy bijekcją wtedy i tylko wtedy, gdy jest funkcją różnowartościową oraz „na”, czyli jest zarówno iniekcją jak i suriekcją jednocześnie.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

f

A

A

y = 3

, ∈ R

x

x

f( ) = f( )

x

x

x

=

x

f( ) =

x

3

f( ) =

x

3

f( ) = f( )

x

x

3

=

3

=

log

3

log

3

= x

log

a

a > 0 a ≠ 1

2 + 5 = 2 + 5

x

x

2 = 2

x

x

=

x

x

f : X → Y

Data generacji dokumentu: 2019-04-15 02:46:27

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=b43249428ccdce76fae169805dc93858