Ekstrema lokalne. Wartość najmniejsza i największa funkcji

(1)

Ekstrema lokalne. Wartość

najmniejsza i największa

funkcji

Autorzy:

Ilona Michalik

2019

(2)

Ekstrema lokalne. Wartość najmniejsza i największa funkcji

Autor: Ilona Michalik

Pochodna funkcji może służyć nam do szukania ekstremów (czyli minimów i maksimów) funkcji. Wiele zadań optymalizacyjnych można rozwiązać właśnie wyznaczając ekstrema.

DEFINICJA

Definicja 1: Minimum lokalne

Funkcja ma w punkcie minimum lokalneminimum lokalne (minimum lokalne właściweminimum lokalne właściwe), jeżeli istnieje taka, że dla każdego zachodzi nierówność ( ).

UWAGA

Uwaga 1:

Przypomnijmy, że symbol oznacza sąsiedztwo punktu o promieniu dodatnim , czyli .

PRZYKŁAD

Przykład 1:

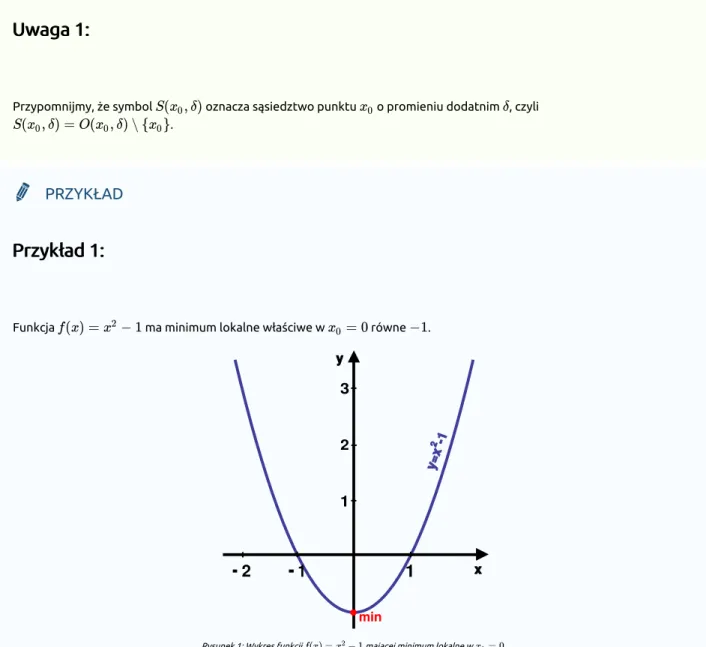
Funkcja ma minimum lokalne właściwe w równe .

-

2 -

1

2

3

y x y=x 2 -1 min

Rysunek 1: Wykres funkcji mającej minimum lokalne w .

f

x

0

∈ R

δ > 0

x ∈ S( , δ)

x

0

f(x) ≥ f( )

x

0

f(x) > f( )

x

0

S( , δ)

x

0

x

0

δ

S( , δ) = O( , δ) ∖ { }

x

0

x

0

x

0

f(x) =

x

2

− 1

_x

₀

_{= 0}

₋₁

f(x) =x2− 1 _x _{= 0} 0

(3)

DEFINICJA

Definicja 2: Maksimum lokalne

Funkcja ma w punkcie maksimum lokalne (maksimum lokalne właściwe)maksimum lokalne (maksimum lokalne właściwe), jeżeli istnieje taka, że dla każdego zachodzi nierówność ( ).

PRZYKŁAD

Przykład 2:

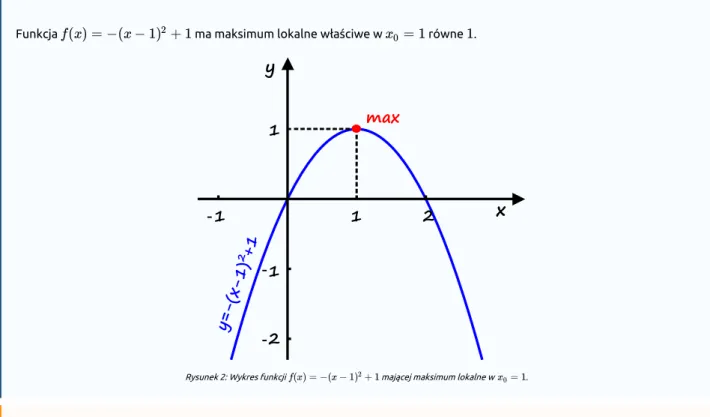
Funkcja ma maksimum lokalne właściwe w równe .

Rysunek 2: Wykres funkcji mającej maksimum lokalne w .

TWIERDZENIE

Twierdzenie 1: Warunek konieczny istnienia ekstremum

Jeżeli funkcja ma ekstremum lokalne w oraz istnieje pochodna funkcji w punkcie , to .

f

x

0

∈ R

δ > 0

x ∈ S( , δ)

x

0

f(x) ≤ f( )

x

0

f(x) < f( )

x

0

f(x) = −(x − 1 + 1

)

2

_x

₀

_{= 1}

₁

f(x) = −(x − 1 + 1)2 _x _{= 1} 0

f

x

0

f

x

0

f

′

( ) = 0

x

0

(4)

UWAGA

Uwaga 2:

Z warunku koniecznego wnioskujemy, że funkcja może mieć ekstrema lokalne tylkotylko w punktach, w których pochodna jest równa zero lub w punktach, w których pochodna nie istnieje.

PRZYKŁAD

Przykład 3:

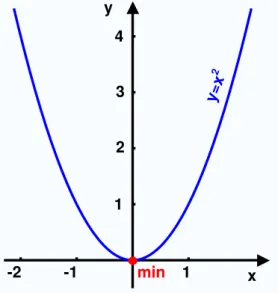
Pochodna funkcji wynosi i zeruje się w punkcie . W tym punkcie funkcja ma minimum lokalne.

4

3

2

1 -2

-1

1 _x

y

min

y=

x

2

Rysunek 3: Wykres funkcji mającej minimum lokalne w punkcie .

f(x) = x

2

_f

′

_{(x) = 2x}

_x

₀

_{= 0}

f(x) = x2 _x _{= 0}

(5)

PRZYKŁAD

Przykład 4:

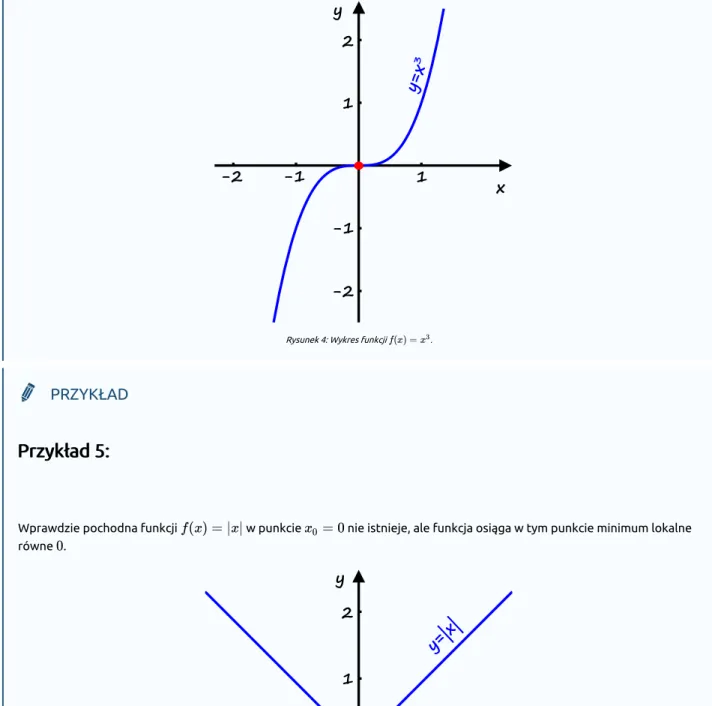
Natomiast pochodna funkcji jest równa i zeruje się w punkcie , ale pomimo to funkcja nie ma w tym punkcie ekstremum.

Rysunek 4: Wykres funkcji .

PRZYKŁAD

Przykład 5:

Wprawdzie pochodna funkcji w punkcie nie istnieje, ale funkcja osiąga w tym punkcie minimum lokalne równe .

Rysunek 5: Wykres funkcji mającej minimum lokalne w punkcie .

f(x) = x

3

_f

′

_{(x) = 3}

_x

2

_x

₀

_{= 0}

f(x) = x3

f(x) = |x|

x

0

= 0

0

(6)

TWIERDZENIE

Twierdzenie 2: I warunek wystarczający istnienia maksimum lokalnego

Jeżeli funkcja , różniczkowalna w otoczeniu , spełnia warunki

1. ,

2. istnieje taka, że dla każdego : oraz dla każdego : , to funkcja ma w punkcie maksimum lokalne.

TWIERDZENIE

Twierdzenie 3: I warunek wystarczający istnienia minimum lokalnego

Jeżeli funkcja , różniczkowalna w otoczeniu , spełnia warunki

1. ,

2. istnieje taka, że dla każdego : oraz dla każdego : , to funkcja ma w punkcie minimum lokalne.

UWAGA

Uwaga 3:

Zamiast założenia wystarczy przyjąć, że funkcja jest ciągła w punkcie . Dzięki temu możemy powyższe twierdzenie zastosować również w przypadku, gdy pochodna nie istnieje w danym punkcie. Jednak ciągłość funkcji w punkcie jest tutaj bardzo ważna.

f

x

0

( ) = 0

f

′

_x

₀

δ > 0

x ∈ S( , δ)

x

−₀

_f

′

_{(x) > 0}

_{x ∈ S( , δ)}

_x

+₀

_f

′

_{(x) < 0}

f

x

0

f

x

0

( ) = 0

f

′

_x

₀

δ > 0

x ∈ S( , δ)

x

−₀

_f

′

(x) < 0

_{x ∈ S( , δ)}

_x

+₀

_f

′

(x) > 0

f

x

0

( ) = 0

f

′

_x

₀

_f

_x

₀

x

0

(7)

PRZYKŁAD

Przykład 6:

Sprawdźmy czy funkcja ma ekstrema lokalne. W tym celu obliczamy pochodną funkcji i wyznaczamy punkty, w których pochodna zeruje się lub nie istnieje.

Dla spełniony jest warunek konieczny istnienia ekstremum lokalnego. Sprawdzamy warunek wystarczający.

Wynika stąd, że funkcja ma w punkcie minimum lokalne i jest ono równe .

TWIERDZENIE

Twierdzenie 4: II warunek wystarczający istnienia maksimum lokalnego

Jeżeli funkcja ma pochodną rzędu w punkcie oraz spełnia następujące warunki:

1. ,

2. ,

3. liczba jest parzysta i ,

to funkcja ma w punkcie ma maksimum lokalne.

f(x) =

x

2

+ 3x − 4

_f

(x) = 2x + 3,

f

′

(x) = 0 ⇔ x = − .

f

′

3

2 = −

x

0 32

(x) > 0 ⇔ x > − ,

f

′

3

2 (x) < 0 ⇔ x < − .

f

′

3

2 f

x

0

= −

3₂

f(− ) = −

3₂ 25₄ f(x) =x2+ 3x − 4

f

n

x

0

( ) = ( ) = ⋯ =

= 0

f

′

_x

₀

_f

′′

_x

₀

_f

(n−1)

( ) < 0

f

(n)

_x

₀

n ∈ N

n ≥ 2

f

x

0

(8)

TWIERDZENIE

Twierdzenie 5: II warunek wystarczający istnienia minimum lokalnego

1. ,

2. ,

3. liczba jest parzysta i ,

to funkcja ma w punkcie ma minimum lokalne.

TWIERDZENIE

Twierdzenie 6: o braku ekstremum

1. ,

2. ,

3. liczba jest nieparzysta i , to funkcja nie ma w tym punkcie ekstremum.

f

n

x

0

( ) = ( ) = ⋯ =

= 0

f

′

_x

₀

_f

′′

_x

₀

_f

(n−1)

( ) > 0

f

(n)

_x

₀

n ∈ N

n ≥ 2

f

x

0

f

n

x

0

( ) = ( ) = ⋯ =

= 0

f

′

_x

₀

_f

′′

_x

₀

_f

(n−1)

( ) ≠ 0

f

(n)

_x

₀

n ∈ N

n > 2

(9)

PRZYKŁAD

Przykład 7:

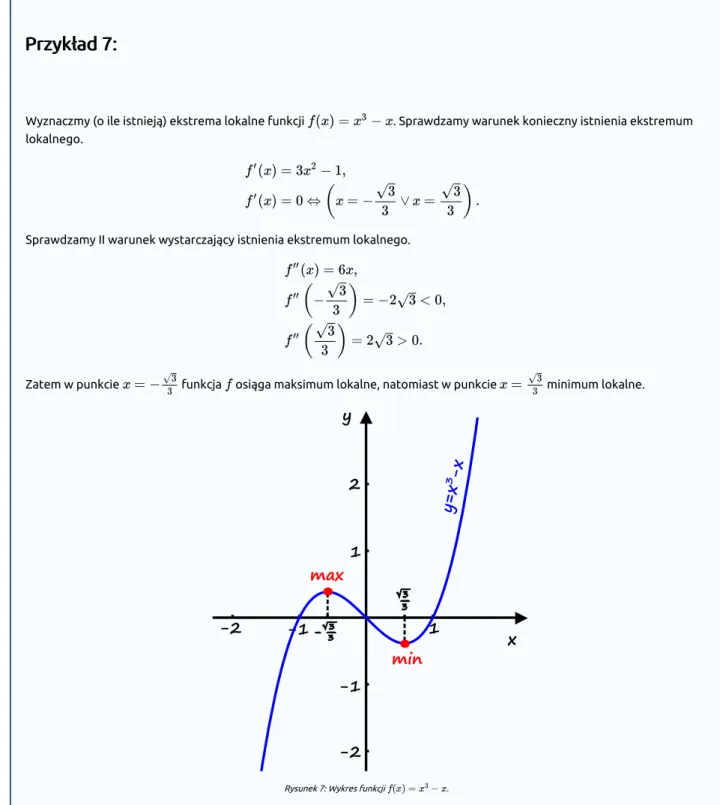
Wyznaczmy (o ile istnieją) ekstrema lokalne funkcji . Sprawdzamy warunek konieczny istnienia ekstremum lokalnego.

Sprawdzamy II warunek wystarczający istnienia ekstremum lokalnego.

Zatem w punkcie funkcja osiąga maksimum lokalne, natomiast w punkcie minimum lokalne.

f(x) =

x

3

− x

(x)

f

′

(x)

f

′

= 3 − 1,

x

2

= 0 ⇔ (x = −

√

₃

3 ∨ x =

√

₃

3 ) .

(x) = 6x,

f

′′

(−

) = −2

< 0,

f

′′

√

3

3 √

3 (

) = 2

> 0.

f

′′

√

3

3 √

3 x = −

√₃3

f

x =

√₃3 f(x) =x3− x

(10)

ZADANIE

Zadanie 1:

Treść zadania: Treść zadania:

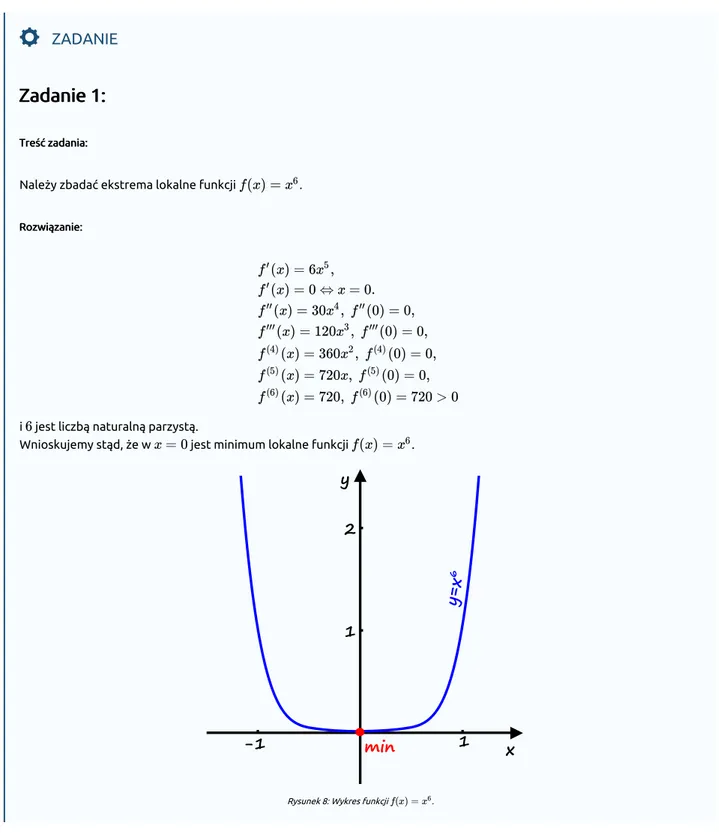
Należy zbadać ekstrema lokalne funkcji .

Rozwiązanie: Rozwiązanie:

i jest liczbą naturalną parzystą.

Wnioskujemy stąd, że w jest minimum lokalne funkcji .

DEFINICJA

Definicja 3: Wartość najmniejsza w zbiorze

Liczba jest wartością najmniejszą funkcji wartością najmniejszą funkcji w zbiorze w zbiorze zawartym w dziedzinie funkcji, jeżeli istnieje takie, że i dla każdego zachodzi nierówność .

f(x) = x

6

(x) = 6 ,

f

′

_x

5

(x) = 0 ⇔ x = 0.

f

′

(x) = 30 ,

(0) = 0,

f

′′

_x

4

_f

′′

(x) = 120 ,

(0) = 0,

f

′′′

_x

3

_f

′′′

(x) = 360 ,

(0) = 0,

f

(4)

_x

2

_f

(4)

(x) = 720x,

(0) = 0,

f

(5)

_f

(5)

(x) = 720,

(0) = 720 > 0

f

(6)

_f

(6)

6 x = 0

f(x) = x

6 f(x) = x6

m ∈ R

f

A

x

0

∈ A

f( ) = m

x

0

x ∈ A

f(x) ⩾ m

(11)

DEFINICJA

Definicja 4: Wartość największa w zbiorze

Liczba jest wartością największą funkcji wartością największą funkcji w zbiorze w zbiorze zawartym w dziedzinie funkcji, jeżeli istnieje takie, że i dla każdego zachodzi nierówność .

Wartość najmniejsza funkcji w zbiorze jest też nazywana minimum globalnymminimum globalnym funkcji w zbiorze , a wartość największa w zbiorze - maksimum globalnym w zbiorze maksimum globalnym w zbiorze .

Algorytm wyznaczania wartości najmniejszej i największej funkcji

Algorytm wyznaczania wartości najmniejszej i największej funkcji ciągłej w przedziale ciągłej w przedziale :: 1. znajdujemy punkty zerowania się pochodnej w przedziale ,

2. znajdujemy punkty w których pochodna nie istnieje w przedziale ,

3. obliczamy wartości funkcji w punktach oraz w punktach uzyskanych w krokach 1 i 2, 4. spośród otrzymanych wartości wybieramy wartość najmniejszą i największą.

UWAGA

Uwaga 4:

Z twierdzenia Weierstrassa mamy pewność, że funkcja ciągła w przedziale przyjmuje wartość najmniejszą i największą w tym przedziale. W przypadku przedziału otwartego nie mamy gwarancji, że takie wartości są osiągane.

M ∈ R

f

A

x

0

∈ A

f( ) = M

x

0

x ∈ A

f(x) ⩽ M

A

f

[a, b]

(a, b)

f

a, b

[a, b]

(12)

PRZYKŁAD

Przykład 8:

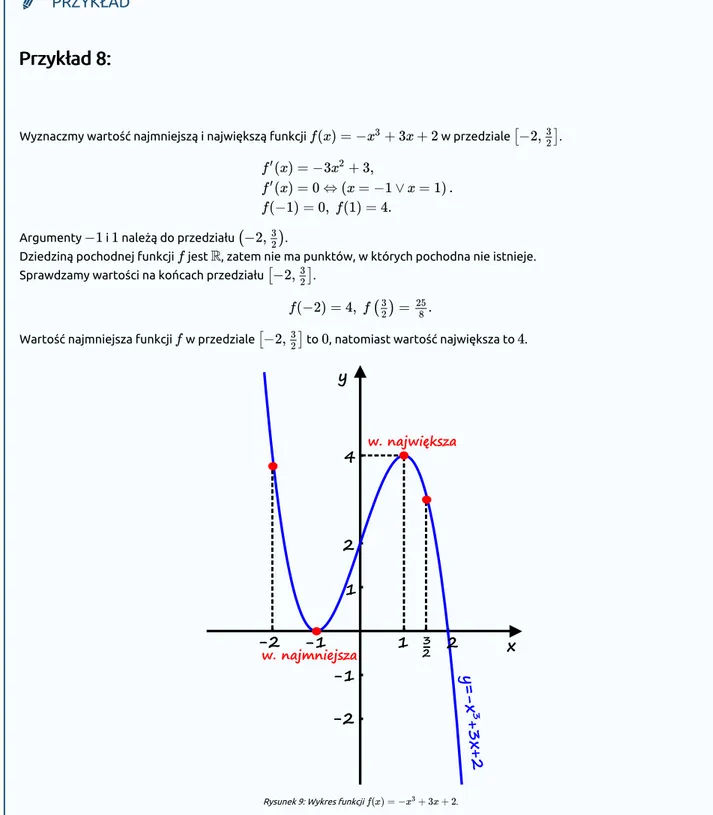
Wyznaczmy wartość najmniejszą i największą funkcji w przedziale .

Argumenty i należą do przedziału .

Dziedziną pochodnej funkcji jest , zatem nie ma punktów, w których pochodna nie istnieje. Sprawdzamy wartości na końcach przedziału .

Wartość najmniejsza funkcji w przedziale to , natomiast wartość największa to .

f(x) = − + 3x + 2

x

3

_{[−2, ]}

3 2

(x) = −3 + 3,

f

′

_x

2

(x) = 0 ⇔ (x = −1 ∨ x = 1) .

f

′

f(−1) = 0, f(1) = 4.

−1 1

(−2, )

3 2

f

R

[−2, ]

3 2

f(−2) = 4, f ( ) = .

3 2 258

f

[−2, ]

3 2

0

4

f(x) = − + 3x + 2x3

(13)

ZADANIE

Zadanie 2:

Treść zadania: Treść zadania:

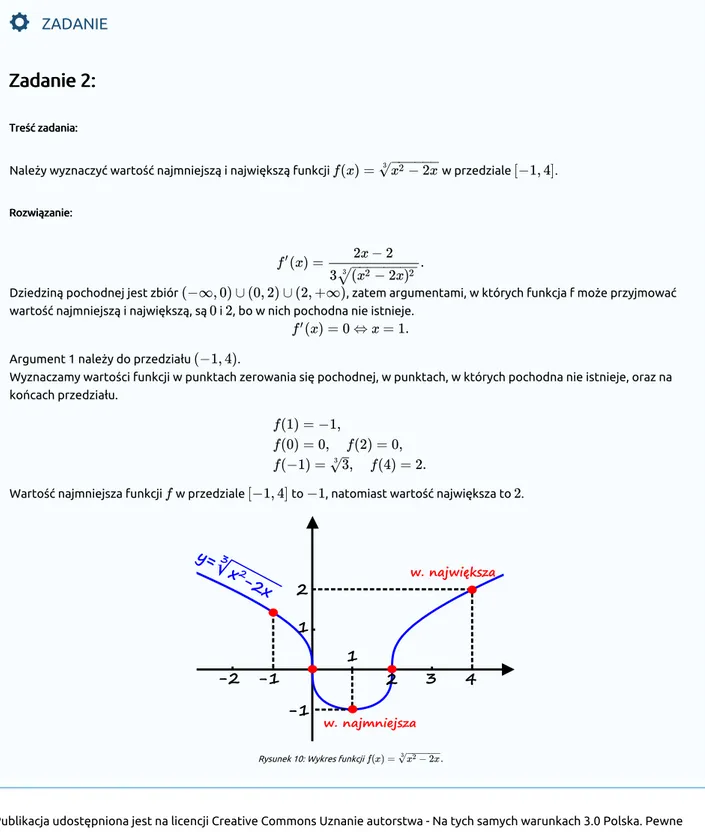
Należy wyznaczyć wartość najmniejszą i największą funkcji w przedziale .

Rozwiązanie: Rozwiązanie:

Dziedziną pochodnej jest zbiór , zatem argumentami, w których funkcja f może przyjmować wartość najmniejszą i największą, są i , bo w nich pochodna nie istnieje.

Argument 1 należy do przedziału .

Wyznaczamy wartości funkcji w punktach zerowania się pochodnej, w punktach, w których pochodna nie istnieje, oraz na końcach przedziału.

Wartość najmniejsza funkcji w przedziale to , natomiast wartość największa to .

Rysunek 10: Wykres funkcji

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 06:10:30

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=918de3a27fac1a8ee511982eb4947461